FCC - Analista Judiciário (TRT 19ª Região)/Apoio Especializado/Estatística/2014
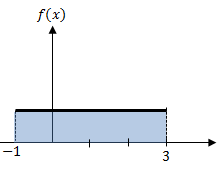
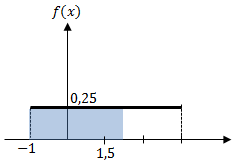




1 - MERCADOS PERFEITAMENTE COMPETITIVOS O modelo de competição perfei…

Em relação à teoria do consumidor, supondo-se curvas de indiferença com i…

1 - O MODELO DE MUNDELL-FLEMING O Pressuposto Fundamental: Economia Ab…

TARIFAS As tarifas são um imposto cobrado quando se quer importar um …

Agências reguladoras, em sentido amplo, seriam órgãos ou entidades co…

1 - EXTERNALIDADES As externalidades podem surgir entre produtores, ent…

Quais instituições compõem o sistema financeiro nacional? Vamos olh…

PARA VER O MAPA COMPLETO, CLIQUE NO LINK ABAIXO:

1 - MERCADOS PERFEITAMENTE COMPETITIVOS O modelo de competição perfei…

Em relação à teoria do consumidor, supondo-se curvas de indiferença com i…

1 - O MODELO DE MUNDELL-FLEMING O Pressuposto Fundamental: Economia Ab…

TARIFAS As tarifas são um imposto cobrado quando se quer importar um …

Agências reguladoras, em sentido amplo, seriam órgãos ou entidades co…

1 - EXTERNALIDADES As externalidades podem surgir entre produtores, ent…

Quais instituições compõem o sistema financeiro nacional? Vamos olh…

PARA VER O MAPA COMPLETO, CLIQUE NO LINK ABAIXO:
Enviar um comentário
0 Comentários