CESPE - Especialista em Previdência Complementar (PREVIC)/Finanças e Contábil/2011

Acerca de finanças, julgue o item.

Quanto à função utilidade e à aversão a risco de um indivíduo, se uma utilidade de Bernoulli u(⋅)$\mathrm{u}(\cdot )$ é convexa, então é correto concluir que o agente é avesso ao risco. Se, por exemplo, uma loteria paga zero com probabilidade 12 ou 1 milhão de reais com probabilidade 12, então o indivíduo é avesso ao risco quando a utilidade média é maior do que a utilidade de Von Neumann-Morgenstern, ou seja,

 

u(12×1milha~o+12×0)>12u(1milha~o)+12u(0)

Resolução:

A primeira parte da afirmativa não confere, conforme podemos verificar das regras abaixo (recomendo a quem queira aprofundar-se no assunto procurar a demonstração gráfica em qualquer bom livro de finanças):

• Se a utilidade de Bernoulli u(·) é côncava (u’’ < 0), então o agente é avesso ao risco.
Ex: u(c) = ln(c), u(c) = c½
 
• Se a utilidade de Bernoulli u(·) é convexa (u’’ > 0), então o agente é amante do risco.
Ex: u(c) = exp(c), u(c) = c2
 
• Se a utilidade de Bernoulli u(·) é linear (u’’ = 0), então o agente é neutro ao risco.
Ex: u(c) = c, u(c) = 10 + 34c

 
A segunda parte da afirmativa confere, ao analisarmos o que costumamos denominar como “a utilidade da média Vs. a média das utilidades”. Isso ocorre, por exemplo, quando atira-se a moeda ao ar, em uma espécie de loteria: Se sai cara, ganha-se 0; se sai coroa, ganha-se 1 milhão.

Então o agente é dito avesso ao risco se

A aversão ao risco assim se constitui porque no caso acima o agente entende que o termo anterior ao “>” (que representa a utilidade da média, ou seja, a utilidade esperada de uma loteria que paga 500 mil com certeza) apresenta maior utilidade que o termo posterior ao dito sinal (“>”), termo este que representa a utilidade média (ou esperada) da loteria (que representa a utilidade de 50% de chance de ganhar um 1 milhão mais a utilidade de 50% de chance de ganhar nada).
 
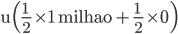
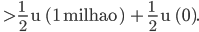
De qualquer modo, estando a primeira parte incorreta, resta que a afirmação como um todo apresenta-se, desta forma,INCORRETA.

Gabarito: Errado