ESAF - Auditor Fiscal da Receita Federal do Brasil/Tributária e Aduaneira/2005

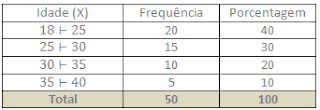
Uma empresa verificou que, historicamente, a idade média dos consumidores de seu principal produto é de 25 anos, considerada baixa por seus dirigentes. Com o objetivo de ampliar sua participação no mercado, a empresa realizou uma campanha de divulgação voltada para consumidores com idades mais avançadas. Um levantamento realizado para medir o impacto da campanha indicou que as idades dos consumidores apresentaram a seguinte distribuição:

Assinale a opção que corresponde ao resultado da campanha considerando o seguinte critério de decisão: 

se a diferença 

X¯¯¯¯−25 for maior que o valor 2σX÷√n então a campanha de divulgação surtiu efeito, isto é, a idade média aumentou; caso contrário, a campanha de divulgação não alcançou o resultado desejado.

Resolução:

Vamos inicialmente calcular a média. Para tanto, consideramos que cada frequência se refere ao ponto médio de classe.

Os pontos médios são:
                                                                  21,5; 27,5; 32,5; 37,5.

Para facilitar os cálculos, vamos trabalhar com a variável auxiliar "d":

d=x−27,55

Os valores de "d" são: 

-1,2; 0; 1; 2

Além disso, podemos dividir todas as frequências por 5. Quando dividimos as frequências por um mesmo número, a média e a variância populacional não se alteram.

Agora calculamos a média e a variância de "d".

Iniciando pela média de "d":

A média de "d" fica:

d¯¯¯=−0,810=−0,08

Lembrando que:

d=x−27,55

Chegamos a:

x=5d+27,5

Do que resulta:

x¯¯¯=5d¯¯¯+27,5

x¯¯¯=5×(−0,08)+27,5=27,1

A média de x é 27,1. O enunciado pede para calcularmos a seguinte quantia:

x¯¯¯−25=27,1−25=2,1

Ficamos entre as alternativas A e C.

Agora calculamos a variância de "d":

Temos:

d2¯¯¯¯¯=11,7610=1,176

Logo, a variância de "d" é dada por:

σ2d=1,176−0,082≈1,176

Notem que o valor 0,08² é muito pequeno, por isso o desprezamos.

Usando as propriedades da variância, podemos achar a variância de x:

x=5d+27,5

σ2x=25×σ2d=25×1,176

O exercício pediu para calcularmos a seguinte quantidade:

2×σxn√

Vamos chamar este valor de "k".

2×σxn√=k

Elevando os dois lados ao quadrado:

4×σ2xn=k2

4×25×1,17650=k2

2×1,176=k2

2,352=k2

Estamos entre as alternativas A e C. Logo, sabemos que k vale 1,41 ou 1,53.

Vamos tomar um valor intermediário, que esteja entre 1,41 e 1,53.

Testando 1,5, temos o seguinte.

1,5 ao quadrado é 2,25, que é menor que 2,352.

Estamos procurando um número que, elevado ao quadrado, seja 2,352. Concluímos que este número deve ser maior que 1,5.

Logo, este número só pode ser 1,53.

Descartamos a letra C e ficamos com a alternativa A.

Gabarito: Letra A