FCC - Analista Judiciário (TRE SP)/Apoio Especializado/Estatística/2012
I. Uma intervenção que afeta uma série temporal pode mudar o nível da série, podendo também afetar a sua variabilidade.Dentre as afirmações acima são verdadeiras APENAS
II. De um modo geral, a análise espectral de séries temporais estacionárias decompõe a série em componentes senoidais com coeficientes aleatórios não correlacionados.
III. Para o modelo Zt = 3 + at − 0,5at − 1, onde at é ruído branco de média zero e variância 2, a previsão de origem t e horizonte 2 é igual a 3 − 0,5at.
IV. Se at é ruído branco de média zero e variância 2 um modelo do tipo:é estacionário de médias móveis sazonal.
a) I e IV.
b) I e III.
c) II e IV.
d) II, III e IV.
e) I e II.
Resolução:
No entanto, pode também ocorrer mudança na variabilidade da série. Sobre o assunto, segue trecho do livro "Análise de Séries Temporais", dos autores Morettin e Toloi:
"Pode haver, também, mudança na variabilidade da série, após a intervenção, bem como um efeito de evolução pode aparecer: a série decai inicialmente e depois retoma o crescimento, até atingir um novo nível".Item certo
Item II. O enunciado é basicamente repetição de outro trecho do mesmo livro já citado no item I:
"De uma forma geral, a análise espectral de séries temporais estacionárias {Zt} decompõe a série em componentes senoidais com coeficientes aleatórios não correlacionados. Juntamente com essa decomposição, existe a correspondente decomposição, em senóides, da função de autocovariância . Assim, a decomposição espectral de um processo estacionário é um análogo à representação de Fourier de funções determinísticas"Item certo
Item III. Vamos representar por:
a previsão de origem t e horizonte h.
Se conhecêssemos todos os valores de , incluindo para os instantes e , teríamos:
Mas as esperanças de e são nulas. Logo:
Item IV. Observem que a sazonalidade ocorre para o operador autorregressivo, não para o operador médias-móveis. Logo, temos um modelo autorregressivo sazonal.


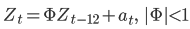









Enviar um comentário
0 Comentários