BACEN - 2010 - CONHECIMENTOS ESPECÍFICOS - ÁREA 2 - QUESTÃO 15
-1 < θ < 1
Mas, o exercício já te diz que θ > 0, então:
0 < θ < 1
Agora que a vaca vai pro brejo! Como calcular isso? Você precisa de duas condições:
Agora, cabe avaliar tais inequações! Quais as condições que λ tem de assumir para ambas serem verdade?
Vamos começar com a equação (1):
Para que isso seja verdade precisamos de uma das duas condições:
(1 - 2λ) > 0 e (λ - 1) > 0
Ou:
(1 - 2λ) < 0 e (λ - 1) < 0
Isso deriva do fato de que na primeira condição o numerador e o denominador são positivos, gerando resultado positivo, enquanto que na segunda ambas as expressões são negativas, gerando resultado negativo.
Para resolver isso, primeira coisa que você tem que fazer é encontrar as raízes de cada uma destas expressões, ou seja, pegue cada uma das expressões (numerador e denominador separadamente), iguale a zero e resolva em função de λ. Vamos lá:
• Se λ < 1/2, o numerador será positivo, enquanto que o denominador será negativo! Isso gera um total negativo! Tente 1/3 para você ver!
• Se 1 > λ > 1/2, o numerador e o denominador serão negativos, gerando o resultado que queremos! Tente λ = 0,9.
• Se λ > 1, o numerador será negativo e o denominador será positivo, gerando resultado negativo! Tente λ = 3!
Viram como realizar a análise da inequação? Vamos fazer isso para a segunda condição:
Vamos isolar toda inequação:
O que gera:
Assim:
Atenção, veja que agora queremos que o conjunto das expressões nos forneça um resultado negativo e não positivo, como no caso anterior. Agora, é só fazer a mesma análise anterior. As raízes dos polinômios são:
2 - 3λ = 0 → λ = 2/3
E:
λ - 1 = 0 → λ = 1
Ao analisar as expressões, precisamos avaliar o sinal da expressão sob as condições λ < 2/3, 1 > λ > 2/3 e λ > 1. Assim:
• Se λ < 2/3, o numerador será positivo, enquanto que o denominador será negativo! Isso gera um total negativo, gerando resultado que queremos! Tente 1/3 para você ver!
• Se 1 > λ > 2/3, o numerador e o denominador serão negativos. Tente λ = 0,9.
• Se λ > 1, o numerador será negativo e o denominador será positivo, gerando resultado negativo, gerando o resultado que queremos! Tente λ = 3.
Portanto, as condições encontradas são:
1) λ < 2/3
2) λ > 1
3) 1 > λ > 1/2
Agora é só pensar! Qual é a alternativa que preenche as duas condições? A intersecção das duas condições, ou seja, a condição que faz com que ambas sejam verdadeiras! Portanto:
2/3 > λ > 1/2





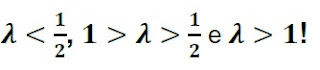














Enviar um comentário
0 Comentários