FCC - Analista Judiciário (TRT 4ª Região)/Apoio Especializado/Estatística/2009

Suponha que o número de partículas emitidas por uma fonte radioativa durante um período de tempo t seja uma variável aleatória com distribuição de Poisson. Sabe-se que a probabilidade de que não haja emissões durante o tempo t é 14. A probabilidade de que haja pelo menos duas emissões durante o tempo t é

a) ln4−1

b) 4−ln4/4

c) ln4/4

d) 1−(ln4/4)

e) 3−ln4/4

Resolução:

Seja λ a média da variável aleatória. A probabilidade da distribuição de Poisson é dada por:

P(X=k)=e−λλkk!

A probabilidade de 0 ocorrências é 1/4:

P(X=0)=14

e−λ×λ00!=14

e−λ=14

Aplicando o logaritmo dos dois lados da igualdade:

ln(e−λ)=ln(14)

−λ=ln(14)

Guardem essa equação (I), que vamos precisar dela posteriormente.

Podemos trocar 1/4 por 4-1:

−λ=ln(4−1)

Quando temos um expoente dentro do logaritmo, podemos "descer" com ele:

−λ=−ln(4)

λ=ln(4) ...(II)

Guardem esta equação (II), que vamos precisar dela depois.

Neste ponto, é importante lembrar a seguinte propriedade dos logaritmos:

eln(a)=a

Portanto, a partir da equação (I), temos:

e−λ=eln(1/4)=14...(III)

Continuando.

Agora calculamos a probabilidade de 1 emissão:

P(X=1)=e−λ×λ11!

Lembrando que e−λ=1÷4  (equação III) e que λ=ln4 (equação II), temos:

P(X=1)=14×ln(4)

Pronto. Já tendo as probabilidades de X = 1 e de X = 0, podemos finalmente responder à questão.

Seja "A" o evento que ocorre quando temos 0 emissões ou 1 emissão:

P(A)=ln44+14

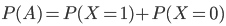
O exercício pediu a chance de 2 ou mais emissões. Ou seja, pediu a chance do evento complementar de "A":

P(A¯¯¯¯)=1−P(A)

=1−ln44−14
=34−ln(4)4

=3−ln(4)4

Gabarito: E