CESPE - Analista do Banco Central do Brasil/Área 4 - Contabilidade e Finanças/2013
seja a média amostral, julgue o próximo item.
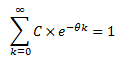






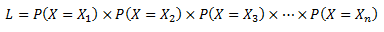








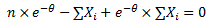







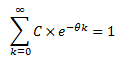






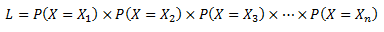








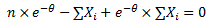







1 - MERCADOS PERFEITAMENTE COMPETITIVOS O modelo de competição perfei…

O art. 5º, I do Decreto-Lei 200/1967 conceitua autarquia da seguinte …

Ocorre crase quando existe a união do artigo ''a' ' com o…

Considere a seguinte curva de possibilidades de produção para uma determi…

1 - MONOPÓLIO Na qualidade de único produtor de determinado bem, o mono…
Julgue o item seguinte, referente à teoria da firma e da produção. …

1 - AS EMPRESAS E SUAS DECISÕES DE PRODUÇÃO A Função de Produção A…

CRÉDITO ESTRUTURADO Ao contrário das formas tradicionais de dívi…

No processo de modernização do Estado, uma das medidas adotadas foi …

Quais instituições compõem o sistema financeiro nacional? Vamos olh…

1 - MERCADOS PERFEITAMENTE COMPETITIVOS O modelo de competição perfei…

O art. 5º, I do Decreto-Lei 200/1967 conceitua autarquia da seguinte …

Ocorre crase quando existe a união do artigo ''a' ' com o…

Considere a seguinte curva de possibilidades de produção para uma determi…

1 - MONOPÓLIO Na qualidade de único produtor de determinado bem, o mono…
Julgue o item seguinte, referente à teoria da firma e da produção. …

1 - AS EMPRESAS E SUAS DECISÕES DE PRODUÇÃO A Função de Produção A…

CRÉDITO ESTRUTURADO Ao contrário das formas tradicionais de dívi…

No processo de modernização do Estado, uma das medidas adotadas foi …

Quais instituições compõem o sistema financeiro nacional? Vamos olh…
Enviar um comentário
0 Comentários