CESPE - Analista (FINEP)/Análise de Projetos /2009 (e mais 1 concurso)

A distribuição populacional dos tempos de duração de um tipo de pilha elétrica é normal com desvio padrão igual a 3 horas, mas com média μ desconhecida. Para se avaliar esse parâmetro desconhecido, foi realizado um experimento, em que foram selecionadas aleatoriamente 9 pilhas elétricas do tipo em questão, registrando-se seus tempos de duração. A média aritmética desses tempos foi igual a 6 horas. Para fins de inferência estatística, foram considerados os seguintes valores aproximados:

Φ$\mathrm{\Phi }$(1,0) = 0,84, 
Φ$\mathrm{\Phi }$(2,0) = 0,98, 
Φ$\mathrm{\Phi }$(3,0) = 0,99,

em que Φ$\mathrm{\Phi }$(z) representa a função de distribuição acumulada da distribuição normal padrão.

 

 

Com respeito ao teste cujas hipóteses nula e alternativa são, respectivamente, H 0: μ > 7 horas e H A: μ < 7 horas, assinale a opção correta. 

a) Se o nível de significância do teste for igual a 5%, então a hipótese nula deve ser rejeitada. 

b) O erro padrão da média amostral é igual a 3 horas. 

c) O nível descritivo do teste é igual a 1%. 

d) O poder (ou potência) do teste independe do tamanho da amostra. 

e) Se a probabilidade de se cometer o erro do tipo I for igual a 0,02 e μ for igual a 3, então a probabilidade de se cometer o erro do tipo II também será igual a 0,02.

Resolução:

O erro padrão da média amostral é dado por:

 

σX¯¯¯¯¯=σn√

 

Em que n$n$ é o tamanho da amostra e σ$\sigma$ é o desvio padrão da população.

 

σX¯¯¯¯¯=39√=1

 

O desvio padrão da média amostral (também chamado de erro padrão) vale 1 hora, e não 3 horas. Errada a letra B.

 

Vamos agora testar a letra C. Nível descritivo é numericamente igual à área delimitada pela estatística teste.

 

A estatística teste fica:

 

X¯¯¯¯¯−μσX¯¯¯

 

=6−71

 

=−1

 

Logo, o nível descritivo, também chamado de p-valor, fica:

 

pv=P(Z<−1)

 

O exercício nos disse que ϕ(1)=0,84. Ou seja:

 

P(Z<1)=0,84

 

∴P(Z>1)=1−0,84

 

P(Z>1)=0,16

 

Por conta da simetria da normal reduzida, temos:

 

P(Z<−1)=0,16

 

Logo, o nível descritivo é de 16%.

 

pv=16%

 

Letra C errada.

 

Se o nível de significância for de 5%, então teremos:

 

α<pv

 

5%<16%

 

Quando o nível de significância é menor que o p-valor, não rejeitamos H0. Errada a letra A.

 

A letra "D" diz que o poder do teste não depende do tamanho da amostra. Isso está errado. O poder do teste é a probabilidade de rejeitarmos H0, dado que é falsa. Neste cálculo, estamos lidando com a distribuição da média amostral, que, após sua normalização, fica:

 

X¯¯¯¯¯−μσ÷n√

 

Notem que o tamanho da amostra aparece sim na fórmula da variável que estamos estudando. Portanto, ele terá impacto sim na hora de calcularmos as probabilidades, todas elas, incluindo o poder do teste. Errada a letra D.

 

Por exclusão, letra E correta.

 

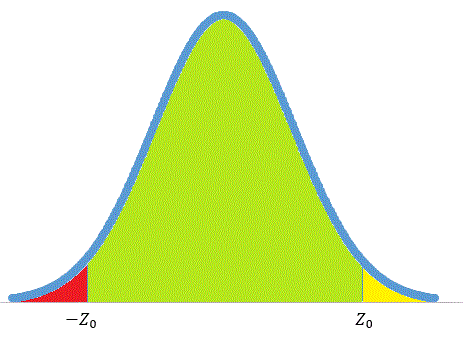
Na letra E, foi dito que o nível de significância é de 2%. Assim, a região crítica, ou seja, aquela na qual rejeitamos H0, tem área de 2%. Trata-se da área vermelha da figura abaixo.

 

 

Detalhe: como a hipótese alternativa é do tipo "a média é menor que alguma coisa", então podemos concluir que a região crítica fica na extremidade esquerda do gráfico.

 

Nossa tarefa agora é calcular −Z0, que é o valor que delimita a região crítica.

 

P(Z<−Z0)=0,02

 

Portanto:

 

P(Z>−Z0)=1−0,02=0,98

 

Dada a simetria da normal:

 

P(Z<Z0)=0,98

 

ϕ(Z0)=0,98

 

Z0=2→−Z0=−2

 

O valor crítico vale -2.

 

O correspondente valor crítico para a média amostral fica assim:

 

Z=X¯¯¯¯¯−μσX¯¯¯

 

−2=X¯¯¯¯¯−71

 

X¯¯¯¯=5

 

O valor crítico é 5. Em outras palavras:

• se a média amostral for maior que 5, aceitamos H0
• se for menor que 5, rejeitamos H0

 

A probabilidade de cometer o erro de tipo II, simbolizada por β$\beta$, corresponde à chance de aceitarmos H0, dado que ela é falsa. No caso da letra E, queremos calcular a chance de aceitarmos H0, dado que a média verdadeira vale 3.

 

A nossa variável normal reduzida será assim construída:

 

Z=X¯¯¯¯¯−μσX¯¯¯

 

E agora não usamos mais μ=7. Isso era feito quando estávamos sob H0. Agora usaremos μ=3, que é a média verdadeira

 

Z=5−31=2

 

Nós aceitaremos H0 quando a média amostral for maior que 5, o que implicará em Z>2

 

β=P(Z>2)

 

β=1−ϕ(2)

 

β=1−0,98

 

β=0,02

 

Alternativa "E" correta.

Gabarito: Letra E