Considere decisões de investimento em um ambiente com risco, em que o agente possui a função utilidade de Bernoulli u(x)=x−−√, e nível de riqueza igual a 5 unidades. Com base nessas informações, julgue o item seguinte.
Considere a loteria cujo lucro seja igual a 36, com probabilidade igual a 12, e lucro igual a 16, com probabilidade igual a 12. Nessa situação, o prêmio de probabilidade do agente sobre a loteria é igual a 26−5√2, ao passo que o prêmio de risco é igual a 1.
Resolução:
A questão apresenta uma função de utilidade de Bernoulli, indicando que o indivíduo é avesso ao risco. Ou seja, o indivíduo prefere receber uma utilidade certa a participar de uma loteria que fornece uma utilidade incerta a ele.
Antes de procedermos aos cálculos, cabe definir os dois conceitos apresentados pela questão:
Primeiramente, vamos calcular o prêmio de probabilidade.
Para tanto, precisamos achar a probabilidade da loteria e depois deduzir este valor da riqueza certa do indivíduo. Utilidade esperada da loteria lucro seja igual a 36, com probabilidade igual a ½ , e lucro igual a 16, com probabilidade igual a ½:
Agora, é preciso encontrar deduzir o valor esperado da loteria pelo valor certo de utilidade, na forma da função de utilidade apresentada:
Agora, devemos encontrar o prêmio de risco, que, para um indivíduo avesso ao risco, sempre possui valor positivo. O sujeito sempre está disposto a pagar algum montante para se ver livre do risco.
Matematicamente, o prêmio de risco pode ser obtido a partir da seguinte expressão:
Prêmio de Risco = Equivalente Certeza - Valor Esperado Loteria
GABARITO: CERTO
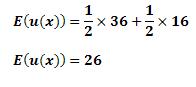














Enviar um comentário
0 Comentários