ESAF - Analista de Comércio Exterior/2002

O texto seguinte diz respeito à questão.

Com o objetivo de avaliar os efeitos das variáveis preço e renda no consumo per capita do setor têxtil de determinado país, ajustou-se, utilizando-se para esse fim observações de 20 anos, o modelo de regressão linear

ln(Ct)=α+βln(Pt)+γln(Rt)+εt        t=1,...,20

onde ln representa o logaritmo neperiano e, com base em t=1, Ct é um índice de consumo per capita, Pt é o quociente de um índice de preço do vestuário pelo índice de custo de vida, Rt é a renda real per capita, α, β e γ são parâmetros desconhecidos e os εt são realizações independentes de uma variável aleatória normal com média zero e variância desconhecida σ2>0.

O ajuste do modelo de regressão linear foi levado a efeito condicionalmente às observações de Pt e Rt que deste modo são tratadas como fixas. As estimativas dos parâmetros, de seus desvios padrão bem como parte da tabela de análise de variância são dados a seguir:

Sabe-se que a estimativa da variância do preditor do valor esperado de ln(C) para um determinado par (P,R) de preço e renda é 0,024. Assinale a opção que dá o valor da estimativa da variância do erro de previsão da observação individual de  ln(C) correspondente à mesma observação de preço e renda.

a) 0,017 

b) 0,001 

c) 0,002 

d) 0,041 

e) 0,025

Resolução:

Primeiro vamos calcular o quadrado médio dos residuos.

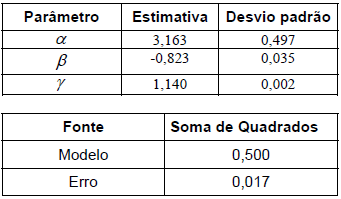
São 20 observações (N = 20). A soma de quadrados total tem 

N−1=20−1=19 graus de liberdade.

São três parâmetros estimados (α, β, γ). Logo, a soma dos quadrados de regressão tem p−1=3−1=2graus de liberdade (onde "p" é justamente a quantidade de parâmetros estimados).

Fazendo a diferença entre as duas quantidades acima, temos o número de graus de liberdade associado à soma dos quadrados dos resíduos:

19−2=17

Dividindo a soma de quadrados dos resíduos (0,017) pelo seu número de graus de liberdade (17), temos o quadrado médio dos resíduos (QMR):

QMR=0,01717=0,001

A variância de ln(Ct) em torno da função de regressão é dada por σ2, que é estimado em 0,001 (= quadrado médio dos reísudos).

A variância da observação individual de ln(Ct) corresponde à soma da variância do preditor do valor esperado (=0,024, conforme enunciado), com a variância em torno da função de regressão (estimada em 0,001). O resultado é:

0,024+0,001=0,025

Gabarito: Letra E