Em um estudo, foram consideradas três variáveis: a oferta de emprego (X1), a oferta de mão-de-obra (X2) e a rotatividade da mão-de-obra (X3). O vetor aleatório
segue uma distribuição normal multivariada cuja matriz de covariância é apresentada a seguir, em que
γij representa a covariância entre Xi e Xj. As médias de X1, X2 e X3 são, respectivamente, iguais a 20, 15 e 30.
A partir dessas informações, julgue o item seguinte.
A variância da soma X1+X2+X3 é igual a 86.
Resolução:
A variância da soma X1+X2+X3 pode ser calculada a partir das propriedades da variância e covariância, como segue.
Var(X1+X2+X3)=Var(X1+X2)+Var(X3)+2Cov(X1+X2,X3) ... (1)
na qual
Var(X1+X2)=Var(X1)+Var(X2)+2Cov)(X1,X2) .... (2)
e
Cov(X1+X2,X3)=Cov(X1,X2)+Cov(X2,X3) .... (3)
A matriz de covariância é tal que
e tem a proriedade se ser simétrica. Dessa forma, a matriz completa de covariância do enunciado pode ser reescrita como
Σ=
Σ=
⎡⎣⎢4−0,47,2−0,41−2,77,2−2,781⎤⎦⎥
Assim, temos
Var(X1)=4
Var(X2)=1
Var(X3)=81
Cov(X1,X2)=−0,4
Cov(X1,X3)=7,2
e
Cov(X2,X3)=−2,7
Substituindo os valores conhecidos em (2) e (3), temos:
Var(X1+X2)=4+1+2×(−0,4)=4,2
e
Cov(X1+X2,X3)=7,2−2,7=4,5
Substituindo os valores conhecidos em (1), temos:
Var(X1+X2+X3)=4,2+81+2×4,5=94,2
Portanto, Var(X1+X2+X3)=94,2
Gabarito: Errado
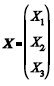
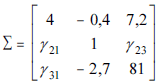













Enviar um comentário
0 Comentários