FCC - Analista Judiciário (TRT 1ª Região)/Apoio Especializado/Estatística/2011

Atenção: A questão refere-se ao gráfico abaixo e à função linear obtida pelo método dos mínimos quadrados, com base em 10 pares de observações (Xi, Yi), i = 1, 2, 3, . . . ,10, sendo X a variável independente e Y a variável dependente. O modelo adotado foi Yi = a + βXi + ∈i, em que a e β são parâmetros desconhecidos e ∈i o erro aleatório com as respectivas hipóteses do modelo de regressão linear simples (a e b são as estimativas de a e β, respectivamente).

Dados: ∑i=110Xi=35,0   e    ∑i=110XiYi=488,1

A variação explicada pelo modelo de regressão apresenta o valor de

a) 23,04. 

b) 57,60. 

c) 207,36. 

d) 230,40. 

e) 288,00.

Resolução:

Em outra questão da mesma prova, o candidato já precisaria ter calculado os valores de "a" e "b". Assim, para resolver a essa questão já se sabe que b = 3,6 e a = -0,3.

Ao final do comentário, mostro a resolução dessa outra questão, indicando como calcular "a" e "b".

Continuando.

A média de X é igual a:

X¯¯¯¯=∑i=110Xi÷10=35÷10=3,5

Substituindo esse valor na reta de regressão, obtemos a média de Y:

Y¯¯¯¯=a+bX¯¯¯¯

Y¯¯¯¯=−0,3+3,6×3,5=12,3

A soma de quadrados do modelo de regressão é dada por:

SQM=b×(∑XY−n×X¯¯¯¯×Y¯¯¯¯)

SQM=3,6×(488,1−10×3,5×12,3)

SQM=3,6×57,6=207,36

Gabarito: Letra C

Segue cálculo de "b":

Para X = 2, temos que Y = 6,9.

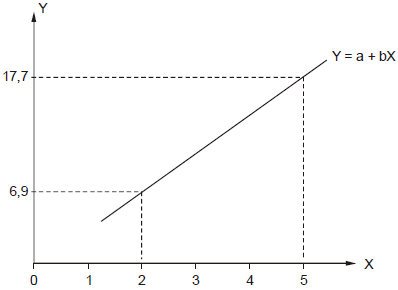
6,9=a+b×2 ...(I)

Para X = 5, Y = 17,7

17,7=a+5b ...(II)

Subtraindo as duas equações:

17,7−6,9=(a+5b)−(a+2b)

10,8=3b

b=10,8÷3=3,6

Voltando em (I):

6,9=a+b×2

6,9=a+3,6×2

a=6,9−7,2=−0,3